问题背景
使用搜索引擎的读者应该都有过这样的体验:当用户在输入框中输入一些关键词或一个词的前半部分时,输入框下方会根据输入内容自动弹出一些推荐搜索的条目供参考
这些智能推荐的搜索词是根据用户以往搜索习惯、关键词热度等多种面参数以及背后的推荐算法自动生成的,那么如何快速根据用户输入内容自动生成推荐搜索词呢?这一讲介绍的Trie树就是适用于这种应用场景的数据结构
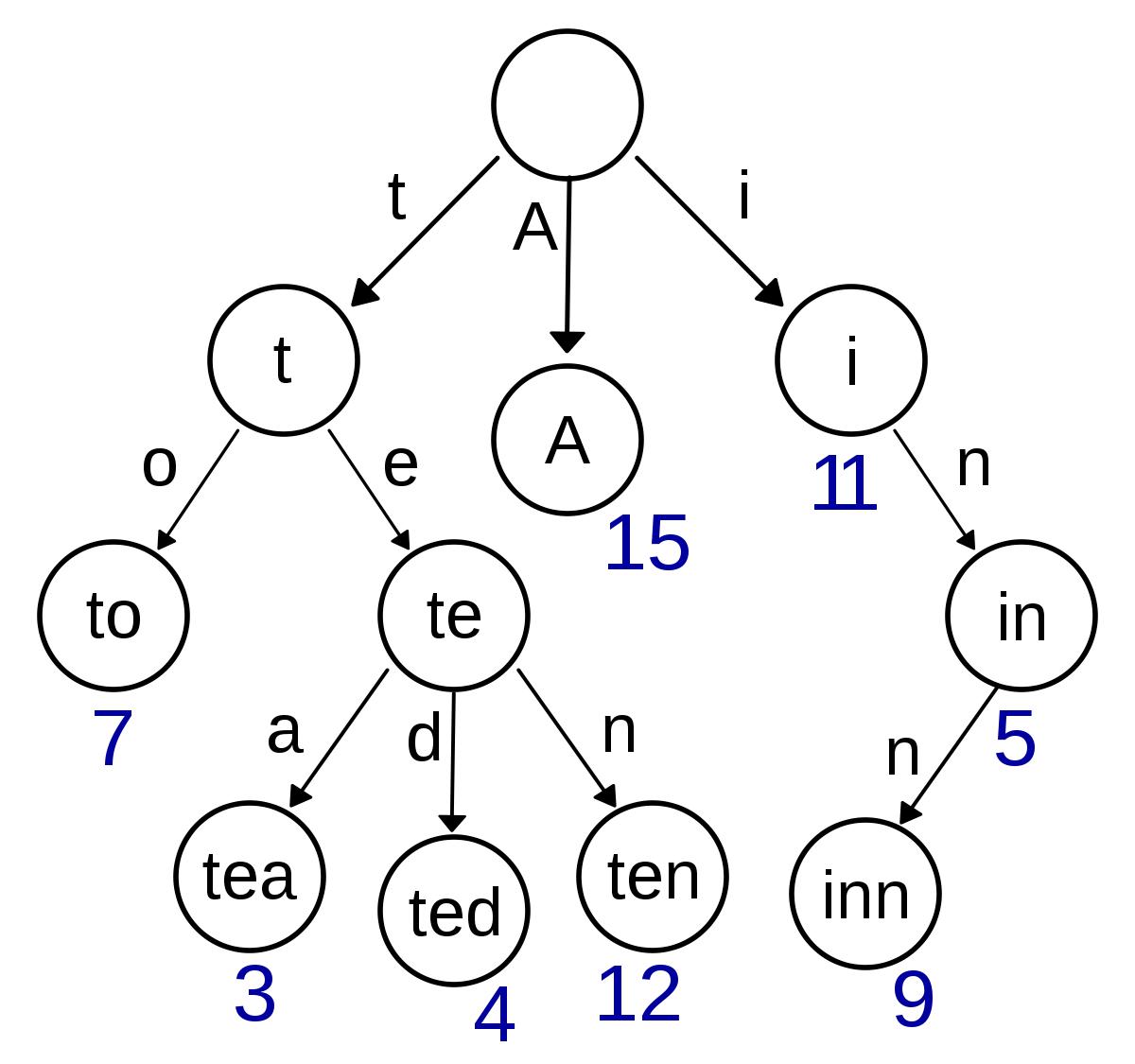
Trie的数据结构
Trie树,即字典树,又称单词查找树或键树,是一种树形结构,一种哈希树的变种,用于高效地存储和检索字符串数据集中的键。
Trie树的典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。
Trie树的基本思想,就是将最终搜索的字符串(单词、词组)散称字母,程序遍历时,根据走过的路径来表示最终得到的单词,表示该单词的叶子结点并不实际存在于Trie树中
单词表建成的Trie树
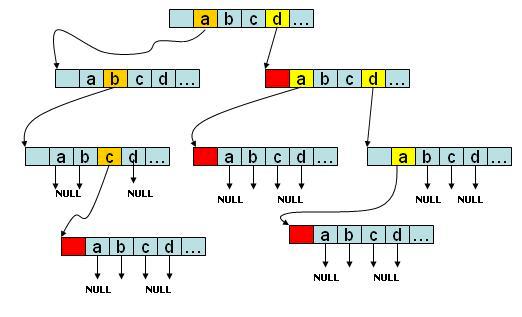
一棵更常见的Trie树
上图所示为一棵实际的Trie树的实际结构:其起点是一个26位字母表,由每位字母延伸出不同的单词。沿着不同的路径向下一路遍历,则得到不同的单词。
Trie的核心思想
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
数据结构定义方法
java版:
static final int ALPHABET_SIZE = 256;
static class TrieNode {
TrieNode[] children = new TrieNode [ALPHABET_SIZE];
boolean isEndOfWord = false;
TrieNode() {
isEndOfWord = false;
for (int i = 0; i < ALPHABET_SIZE;i++){
children[i] = null;
}
}
};
Python版:
class TrieNode:
#Trie node class
def _init___( self):
self.children = [None] * ALPHABET_SIZE
#isEndOfWord is True if node represent
# the end of the word
self.isEnd0fword = False
这里用到的是Python的dictionary
Trie的基本性质
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
实战题目
-
python版:
class Trie(object): def _init_( self): self.root ={} self.end_of_word = "#" def insert(self, word): node = self.root for char in word: node = node.setdefault(char,{0)#如果此处值存在,则取出对应的值,否则将其设置为{} node[self.end_of_word] = self.end_of_word def search(self,word): node = self.root for char in word: if char not in node: return False node = node[char] return self.end_of_word in node#和后面判断是否为前缀区分开来,此处还要判断是否为end_of_word def startswith(self, prefix): node = self.root for char in prefix: if char not in node: return False node = node[char] return Truejava版,与Python思想一致
class TrieNode { public char val; public boolean isword; public TrieNode[] children = new TrieNode[26]; public TrieNode() {} TrieNode(char c){ TrieNode node = new TrieNode( );node.val = c; } } public class Trie { private TrieNode root; public Trie() { root = new TrieNode(); root.val =''; } public void insert(String word){ TrieNode ws = root; for(int i= 0; i < word.length(); i++){ char c = word.charAt(i); if(ws.children[c - 'a' ] == null){ ws.children[c - 'a'] = new TrieNode(c); } ws = ws.children[c - 'a ']; } ws.isword = true; } public boolean search(String word) { TrieNode ws = root; for(int i =0; i < word.length(); i++){ char c = word.charAt(i); if(ws.children[c - 'a' ]== null) return false; ws = ws.children [c - 'a']; } return ws.isword; } public boolean startswith(String prefix){ TrieNode ws = root; for(int i=0; i< prefix.length(); i++){ char c = prefix.charAt(i); if(ws.children[c - 'a' ] ==null) return false; ws = ws.children[c - 'a']; } return true; } }
二维网格中的单词搜索 给定一个单词网格(二维字母数组)和一个单词表数组,返回能够在网格中找到的单词
- 思路一:朴素的DFS,针对输入单词数组中的每个单词,在字符矩阵中进行深度优先搜索
- 思路二:根据输入单词数组建立字典树,树的各边代表一个字母,一条路径就是一个单词。根据预处理生成的字典树再对棋盘进行DFS搜索
- Python版:
dx = [-1,1,0,0]
dy = [0,0,-1,1]#上下左右移动的方向数组
END_OF_WORD ="#"
class solution(object):
def findWords(self, board,words):
if not board or not board [0]: return []
if not words: return []
self.result = set()#最后返回的result是一个set
root = collections.defaultdict()#root作为Trie树根节点
for word in words:#建立字典树,将输入单词数组所有字符插入到字典树中
node = root
for char in word:
node = node.setdefault(char, collections.defaultdict())
node [END_OF_WORD] =END_OF_WORD
self.m, self.n = len(board), len(board[0])
for i in xrange(self.m):
for j in xrange(self.n):
if board[i][j] in root:#字符矩阵中的字符存在字典树中出现,是进行dfs的前提
self._dfs(board, i, j, "", root)
def _dfs(self, board, i, j, cur_word,cur_dict):#cur为遍历单词当前的“形态”,cur_dict为Tire现在遍历到的位置
cur_word += board [i][j]#下一步遍历,后缀加一个字符
cur_dict = cur_dict [board [i][j]]
if END_OF_WORD in cur_dict:
self.result.add ( cur_word)
tmp, board[i][j] = board [i][j], '@'#已遍历到且可行的位置做标记
for k in xrange(4):
x, y = i + dx[k], j +dy[k]#上下左右移动探测
if 0 <= x < self.m and 0 = y < self.n \
and board [x][y] != '@' and board [x][y] in cur_dict:
self._dfs( board,x,y, cur_word,cur_dict)
board[i][j] = tmp
java版:
public class Solution { Set<String> res = new HashSet<String>(); public List<String> findwords(char[][] board,String[] words){ Trie trie = new Trie(); for (String word : words) { trie.insert(word); } int m = board.length; int n = board[0].length; boolean[][] visited = new boolean[m][n];//新开数组visited标记访问而不是修改原数组 for (int i = 0; i<m; i++) { for (int j =0; j <n;j++){ dfs(board,visited,"",i,j, trie); } } return new ArrayList<String-( res); } public void dfs(char[][] board,boolean[][] visited,String str,int x,inty,Trie trie){ if (x<0 || x >= board.length || y<0 || y >= board[0].length) return; if (visited [x][y]) return; str += board [x][yl; if (!trie.startswith(str)) return;//当前单词是存 if (trie.search(str)) { res.add(str); } visited [x][y] = true; dfs(board, visited,str, x-1, y, trie); dfs(board, visited,str, x+1, y, trie); dfs(board, visited,str, x, y-1, trie); dfs(board, visited,str, x, y+1, trie); visited[x][y] = false;//恢复现场,便于后续搜索 } }
- 系统设计——搜索建议