二分查找
适用问题条件：
- Sorted（单调递增或者递减）
- Bounded（存在上下界）
- Accessible by index（能够通过索引访问）
应用举例
下图展示了为从数组（已排序，存在上下界限并能通过索引访问）中查找特定元素的过程：
\_
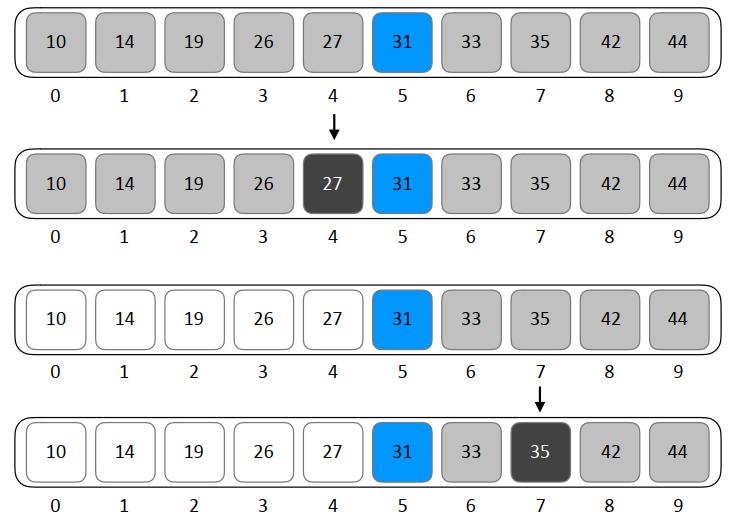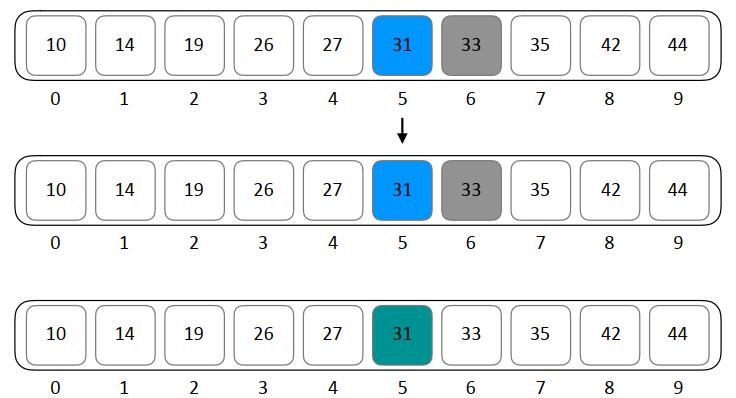二分查找示例
代码模板
left, right = 0, len(array) - 1
while left <= right:
mid = (left + right ) / 2
if array [mid] == target:
// find the target! !
break or return result
elif arraytmid] < target:
left = mid + 1
else:
right = mid - 1
实战题目
- 求sqrt(x)
- 思路一：由于y=sqrt(x)，所以x=y^2，单调递增，因此可以使用二分法进行上下查找。根据输入数字设定上下限，通过比较中间值的平方和输入数的大小，使上下限不断逼近（左右边界差距达到要求的精度）。由于是浮点数，调整边界时交换mid、left与right即可
返回整数：
int sqrt(int x) {
if (x == 0 || x == 1) return x;
int l = 1, r = x, res;
while (l <= r) {
int m = (l +r)/ 2;
if (m == x / m){
return m;
}
else if (m > x / m){
r = m -1;
}
else{
l = m + 1;
res = m;
}
}
return res;
}
- 思路二：使用牛顿迭代法，即利用公式xn+1=xn-f(xn)/f`(xn)，代入此问题（f(x)=x2-y0）得到此问题的迭代公式：xn+1=(xn+y0/xn)/2)不断计算xn+1。当n~+∞，则xn~sqrt(x)。
Python版：
class Solution( object):
def mySqrt(self, x):
r = x#将x0设为右界，保证x0^2大于y0，才有迭代的必要
while r*r > x
r = (r + ×/r)/ 2
return r