并查集是什么

Union & Find，顾名思义，指将两个集合先并在一起，再查找。并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。其中两种常见操作：

Join指将两个子集合并成同一个集合。
Find指确定元素属于哪一个子集。可用来确定两个元素是否属于同一子集。

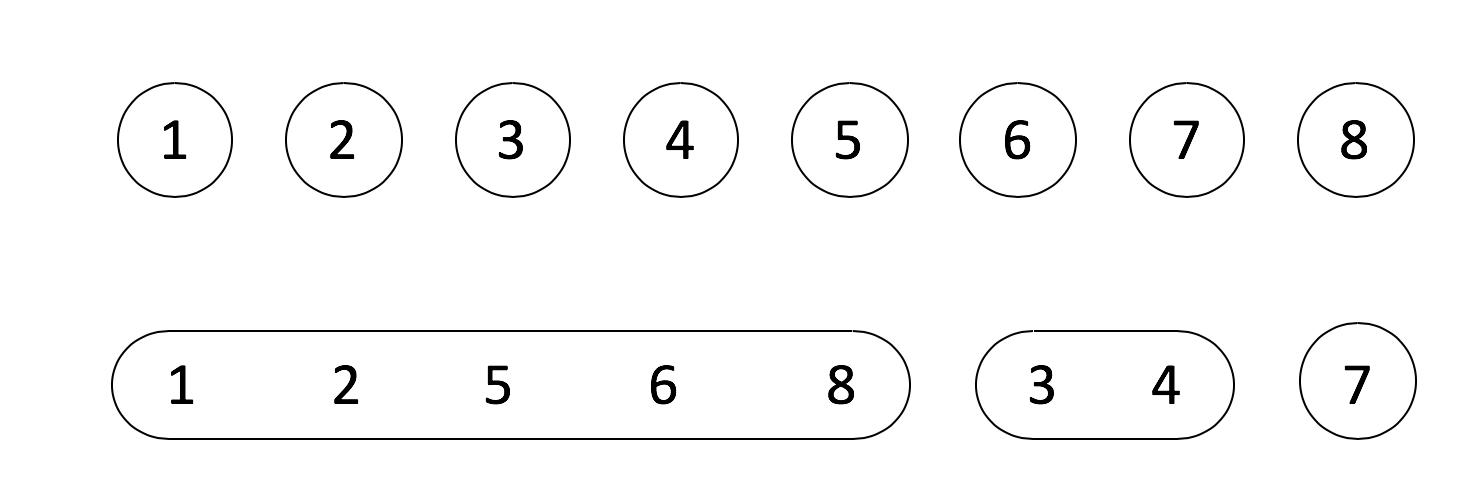并查集Join示意图

举一个生活中的例子：小弟通过报出自己的老大，层层上推，最后归纳出帮派，来识别是否是同一门派

并查集两种优化方式：

小组织（个体）和大组织（组织）的合并
路径压缩，跳过中间的小头目，直接报出帮派boss

数据结构和代码实现方式

数据结构

并查集通常使用数组实现，如下图所示，一个roots数组里面有若干root指针，初始的时候都指向自身，表示集合只有自身一个元素。这种状态是“各自为营”

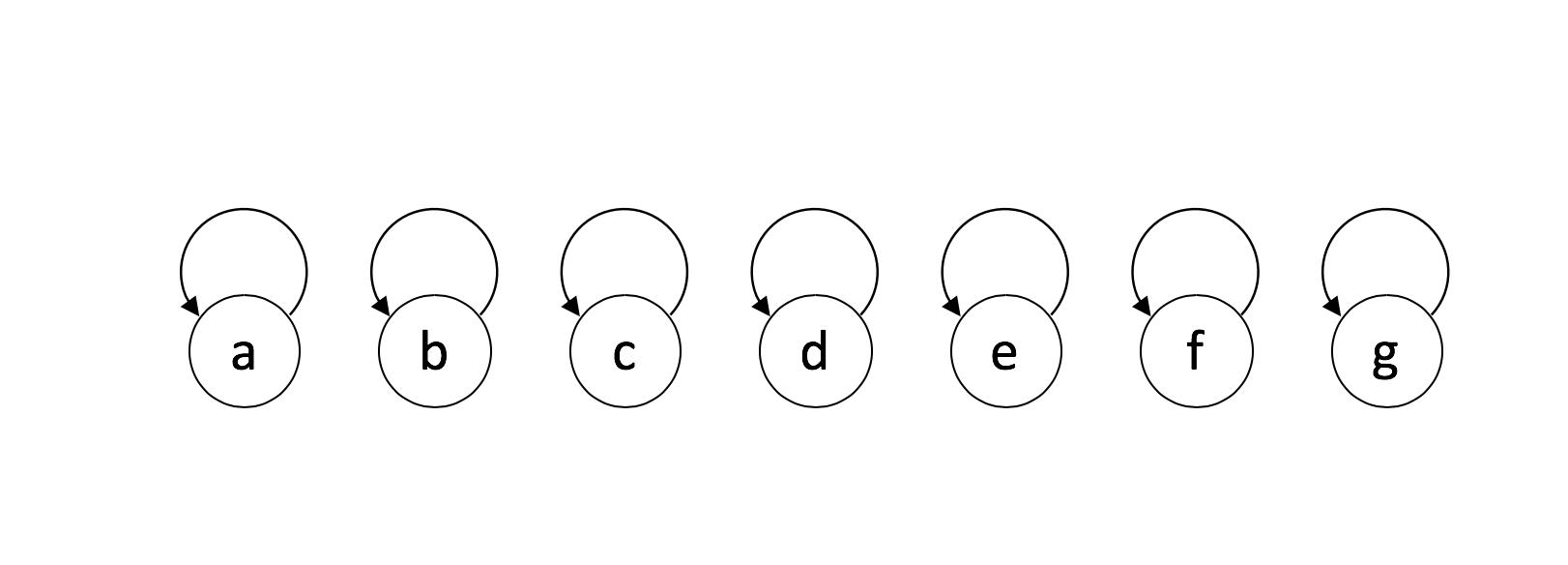并查集初始状态

在对并查集进行若干操作之后，假设并查集的结构如下所示，从d节点的root指针一路向上寻址，最终的节点是a，则a就是左边集合的根节点，右边同理。

代码实现

并查集常用的几个方法：MakeSet、Find和Union可通过如下方式实现：

function MakeSet(x)
    x.parent := x

function Find(x)
    if x.parent == x
        return X
    else
        return Find(x.parent)

function Union(x, y)
    xRoot := Find(x)
    yRoot := Find(y)
    xRoot.parent := yRoot

并查集优化

优化一合并并查集的合并，又可分为两种方式：不带深度的合并和带深度的合并

function MakeSet(x)
    x.parent1 = x
    x.rank := 0

function Union(x, y)
    xRoot := Find(x)
    yRoot := Find(y)
    if xRoot == yRoot
        return

    // x和y不在同一个集合，合并他们。
    if xRoot.rank < yRoot. rank
        xRoot.parent := yRoot
    else if xRoot.rank > yRoot.rank
        yRoot.parent:=xRoot
    else
        yRoot.parent := xRoot
        xRoot.rank := xRoot.rank + 1

优化二路径压缩针对长链等情况，直接去掉中间冗余链接，方便快速找出集合的root

路径压缩示例 </div>

java实现代码：

public class QuickUnionUF{
    private int[] roots;

    public QuickUnionUF(int N){
        roots = new int [N] ;
        for(int i=0;i<N;i++){
            roots[i]=i;
        }
    }

    private int findRoot(int i){
        int root = i;
        while (root != roots[root])
            root = roots [root];
        while (i != roots[i]){
            int tmp =roots[i]; 
            roots [i] = root;
            i = tmp;
        }
        return root;
    }

    public boolean connected(int p,int q){ 
        return findRoot(p) == findRoot(q);
    }

    public void union(int p，int q) {
        int qroot = findRoot(q);
        int proot = findRoot(p);
        roots[proot] = qroot;
    }
}

实战题目

岛屿个数
给定一个二维的数组，0表示海洋，1表示陆地，问二维数组表示的平面中有多少块岛屿
- 思路一：采用染色问题解决的思路，遍历所有节点，发现为1的位置后将与其相邻的块去掉（值变为0），这一步可以采用DFS或BFS
  - Python代码（非侵入性改值，换为用set记录）

class Solution(object):
    dx=[-1,1,0,0]方向数组
    dy=[0,0,-1,1]

    def numIslands(self, grid):
        if not grid or not grid[0]: return 0

        self.max_x = len(grid); 
        self.max_ y = len(grid[0] ); 
        self.grid = grid; 
        self.visited = set()

    return sum([self.floodfill_DFS(i, j) for i in range(self.max_x) for j in range(self.max_y)])
    #或者return sum([self.floodfill_BFS(i, j) for i in range(self.max_x) for j in range(self.max_y)] )

    def floodfill_DFS(self, x, y):
        if not self._is_valid(x, y): return 0
        self.visited.add((x, y))
        for k in range(4):
            self.floodfill_DFS(x + dx[k], y + dy[k] )
        return 1

    def floodfill_BFS(self, x, y):
        if not self._is_valid(x, y): return 0

        self. visited.add((x, y) )
        queue = collections. deque()
        queue.append((x, y))

        while queue:
            cur_x, cur_y = queue.popleft()
        for i in range(4) :
            new_x, new_y = cur_x +dx[i], cur_y + dy[i]
            if self._is_valid(new_x, new_y):
                self.visited.add((new_x, new_y))
                queue.append((new_x, new_y))

        return 1

    def _is_valid(self, X, y):#判断是否为陆地，代码写得十分冗余，可以缩短为一行
       # return  0 <= x <= self.max_x and 0 <= y <= self.max_y and self.grid[x][y] != '0' and ((x, y) not in self.visited)
        if x < 0 or x >= self.max_x or y<0 or y>=self.max_y:#超限
            return False 
        if self.grid[x][y] == '0' or ((x, y) in self.visited) :#非1位置
            return False
        return True

思路二：并查集方式：
1. 首先遍历二维数组，将每个为1的节点初始化为并查集
2. 再遍历值为1的节点，相邻者合并（同时统计parent节点数）
3. 最后遍历一次，统计parent数量
并查集结构的定义：

class UnionFind(object):
    def _init_(self, grid):
        m, n = len(grid), len(grid[0])
        self.count = 0
        self.parent = [-1] * (m*n)
        self.rank = [0] * ( m*n)

        for i in xrange(m):
            for j in xrange(n):
                if grid[i][j] == '1':
                    self.parent[i*n + j] = i*n + j
                    self.count += 1

    def find(self, i):
        if self.parent[i] != i:
            self.parent[i] = self.find(self.parent[i])
        return self.parent[i]

    def union(self, X, y):
        rootx = self.find(x)
        rooty = self.find(y)
        if rootx != rooty: 
            if self.rank[rootx] > self.rank[rooty]:
                self.parent[rooty] = rootx
            elif self.rank[rootx] < self.rank[rooty]:
                self.parent[rootx] = rooty
            else:
                self.parent[rooty] = rootx
                self.rank[rootx] += 1
            self.count -= 1

具体解题代码：

class Solution(object):
    def numIslands(self, grid) :
        if not grid or not grid[0]:
            return 0

        uf = UnionF ind(grid)
        directions = [(0,1), (0,-1), (-1,0), (1,0)]#二元组代替方向数组
        m, n = len(grid), len(grid[0])

        for i in xrange(m): 
            for j in xrange(n):
                if grid[i][j] == '0':
                    continue
                for d in directions:
                    nr,nc=i+d[0],j+d[1]
                    if nr>=0 and nc>=0 and nr<m and nc<n and grid[nr][nc]=='1':#类似于上一题is_valid判断
                        uf.union( i*n+j, nr*n+nc )
        return uf.count

朋友圈
给定一个矩阵，矩阵的两维相同，都表示独立的个体（人），在此矩阵的元素中，0表示陌生，1表示认识，问这个群体中朋友圈的个数有多少（所有直接和间接相识的人之间算一个朋友圈）

并查集