算法学习笔记第三讲

一、优先队列

PriorityQueue

特点：

正常入
按照优先级出

实现机制：

Heap (Binary, Binomial, Fibonacci)
Binary Search Tree

例如小顶堆：

入队，需保持最小元素在堆顶；出队，直接返回堆顶元素

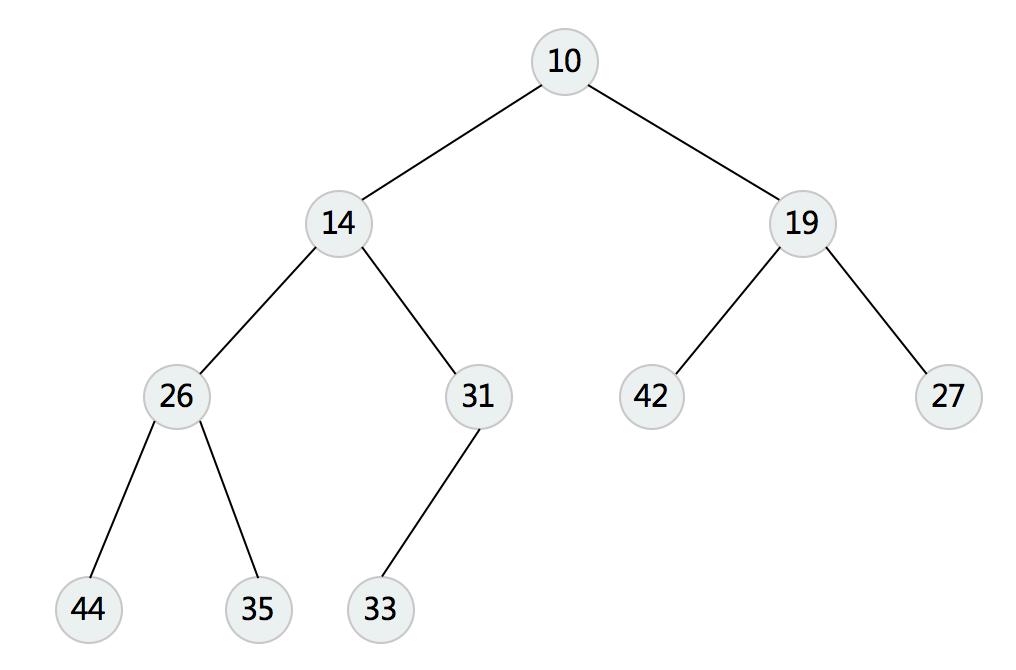
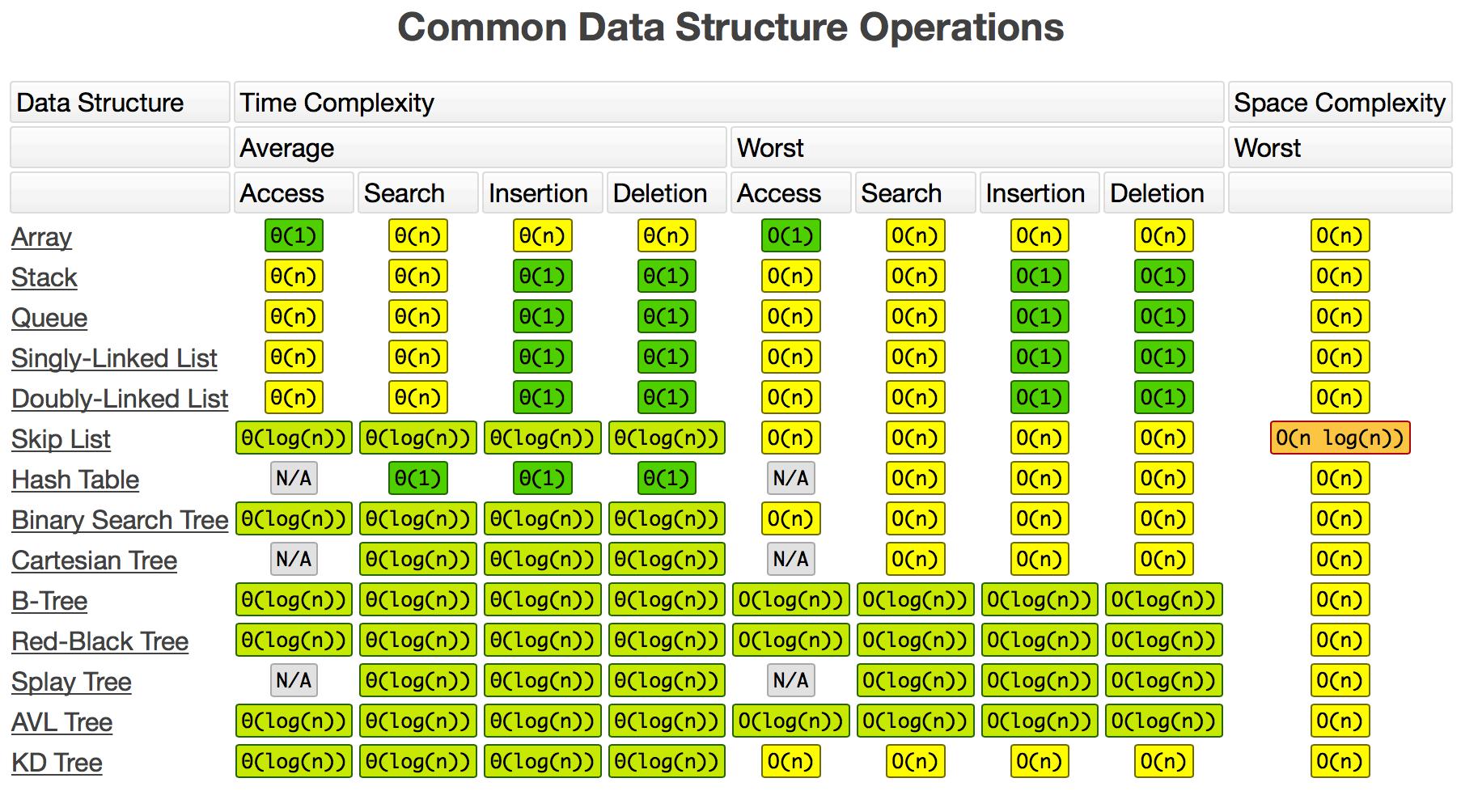
不同实现机制的优先队列，及其基本操作的时间复杂度如下

__无需自己实现一个优先队列，会用就行__

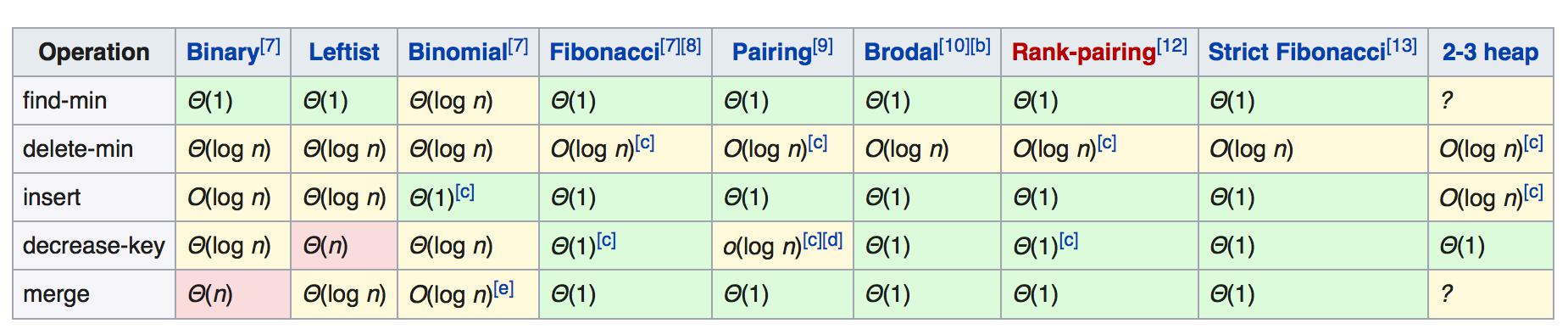
实战题目

第K大的元素

class KthLargest {
    final PriorityQueue<Integer> prq;
    final int k;
    public KthLargest(int k, int[] nums) {
        this.k=k;
        prq=new PriorityQueue<>(k);
        for(int n:nums){
            add(n);
        }
    }

    public int add(int val) {
        if(prq.size()<k){//队列未满，直接插入即可
            prq.offer(val);//offer操作
        }
        else if(val > prq.peek()){
            prq.poll();//已有k个元素，且新元素大于当前最大元素，需将队首弹出再插入，否则无需操作。
            prq.offer(val);
        }
        return prq.peek();//返回队首
    }
}

滑动窗口

思路：

维护一个优先队列（大顶堆），根元素最大。窗口每次滑动调整堆内元素，将堆顶元素放入结果数组。维护堆顶元素最大复杂度LogK，返回最大值复杂度O(1)，总体复杂度O(N·logK)

因为窗口大小固定，且只返回最大值，所以无需优先队列，用队列即可。维护一个deque(双端队列)。首先前k元素进入队列，后面随窗口滑动维护队列。窗口向右滑动时若比队列最大元素小则正常进入，若比最大元素大则移除前面全部元素再入队，始终保持最大元素在最左边。时间复杂度O(N·1)

class Solution(object):
    def maxSlidingWindow(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: List[int]
        """
        if not nums: return []
        window,res=[],[]
        for i,x in enumerate(nums):
            if i >= k and window[0]<= i-k:
                window.pop(0)
            while window and nums[window[-1]] <= x:
                window.pop()
            window.append(i)
            if i >= k-1:
                res.append(nums[window[0]])
        return res

二、映射Map & 集合Set

HashTable & Hash Function & Collisions

什么是Hash函数：

Hash函数能够实现O(1)复杂度的元素查找，实现元素（值）和其存放位置（键）的快速映射

使用ASCII码进行映射的示意图所下所示：

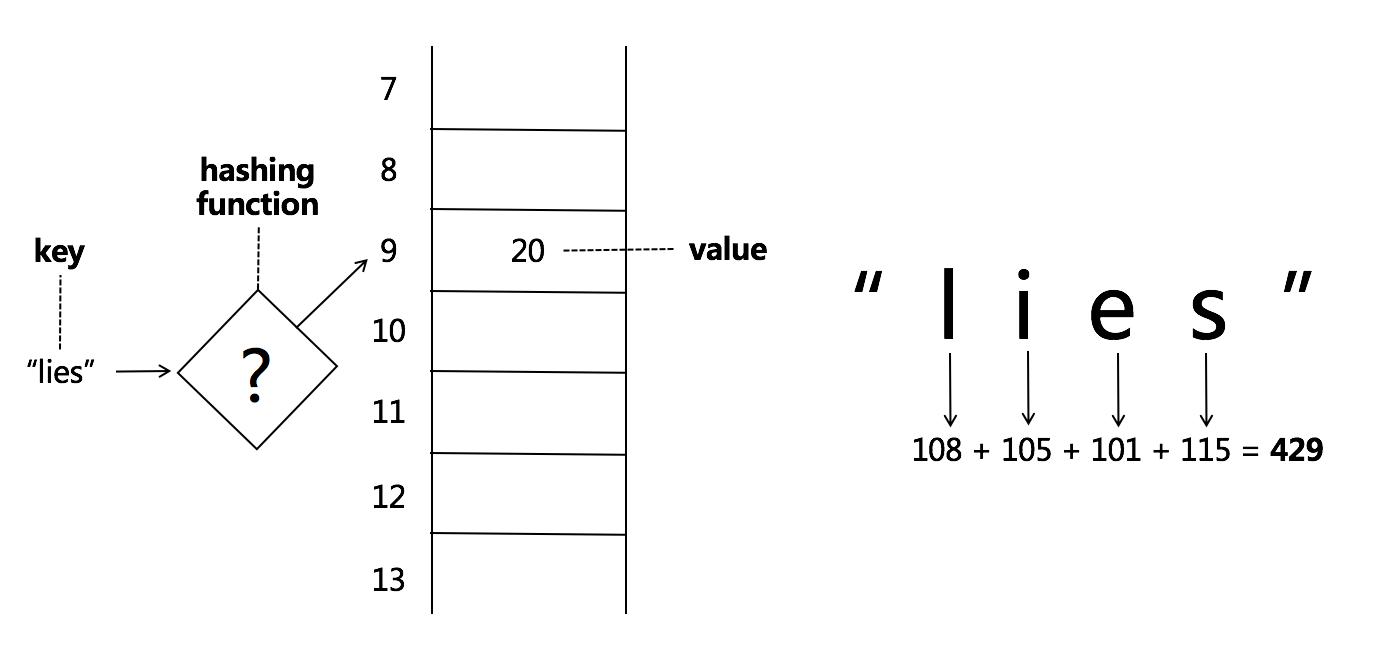
Hash函数的碰撞：不同元素经过相同的哈希函数作用得到了相同的“键”，如果不加处理则映射关系就会失效

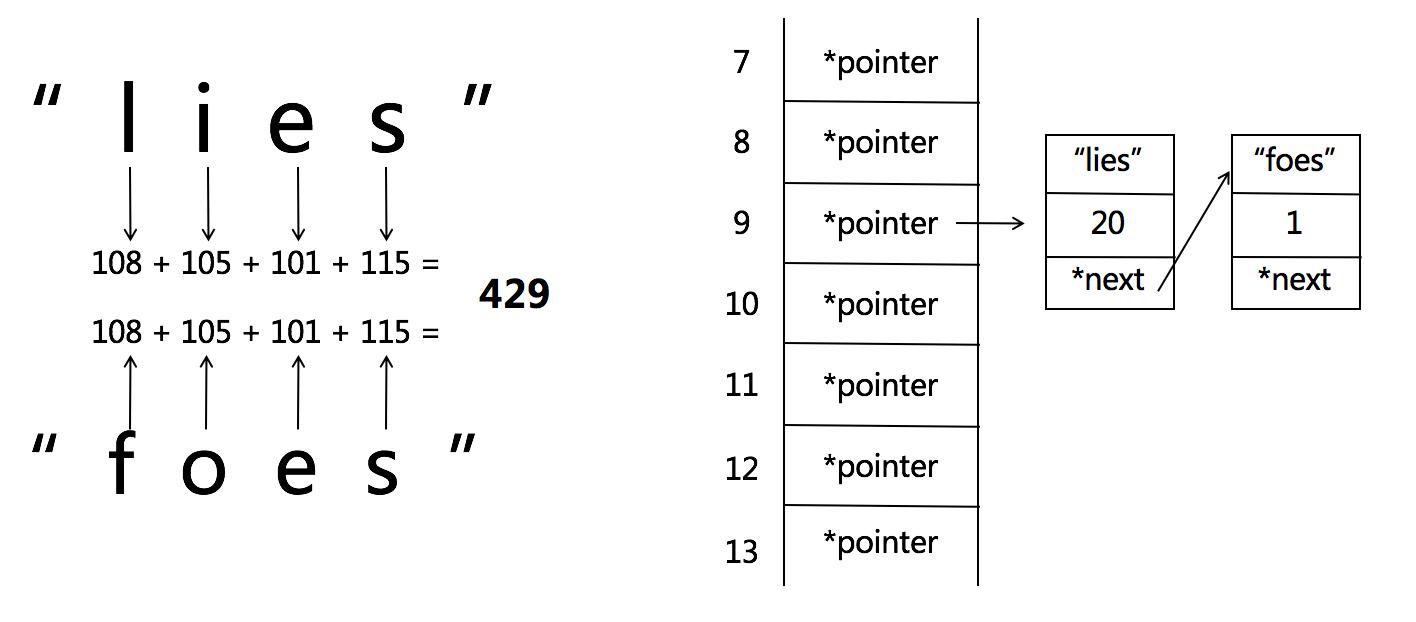
哈希碰撞的几种处理思路：

“拉链法”，在冲突的键处放链表，将相同键的值链接起来
左移，在进行键值映射时，如果发现与前面的映射冲突了，则将此映射关系向前移动固定长度，如果移动后还是与前面的映射冲突，继续移动知道找到唯一的键值对关系
右移，原理与上相同

List vs Map vs Set（抽象数据结构）

List：线性表，元素可重复，数组或链表，查找耗时O(N)，插入O(1);
Map：映射关系，“键——值”的对应关系，键唯一;
Set：集合，可认为是List去重版，但实现机制一般是哈希表或二叉树，查找O(1)或O(logN);

HashMap，HashSet，TreeMap，TreeSet

哈希方式实现的Map和Set，查找复杂度均为O(1)，

Tree方式实现的Map和Set，查找复杂度均为O(LogN)
哈希方式优势在于查找的时间复杂度，Tree方式优势在于元素排列是有序的。
根据实际情况选用不同方式

不同语言HashMap 最佳实践（使用形式）

Python
1. dict
2. hashmap = {key: value}
C++
1. std::unordered_map
2. std::map
Java
1. HashMap
2. TreeMap

不同语言HashSet 最佳实践（使用形式）

Python
1. hashset = {value1, value2}
C++
1. std::unordered_set
2. std::set
Java
1. HashSet
2. TreeSet

实战题目

有效异位词
所谓异位词，指的是单词组成字母相同，但字母移位了的字符串。给定两个字符串，返回true或false

思路一：字符串内字符按字母顺序排序，最后比较字符串是否相同。使用快排最快时间复杂度：O(NlogN)
1
2
def IsAnagram(self,s,t): return sorted(s)==sorted(t)
思路二：哈希函数权值比较。

思路三：数各字符出现次数，每遇到一个字符，其出现次数+1。时间复杂度O(N)

用编程语言自带的map

def isAnagram1(self,s,t):
    dic1, dic2 = {}, {}
    for item in s:
        dic1[item] = dic1.get(item, 0) + 1
    for item in t:
        dic2[item] = dic2.get( item, 0) + 1 
    return dic1 == dic2

或自己用一个26位长度的数组记录：

def isAnagram2(self,S,t):
    dic1, dic2 = [0]*26, [0]*26
    for item in s:
        dic1[ord(item)-ord('a')] += 1
    for item in t:
        dic2 [ord(item)-ord('a')] += 1
    return dic1 == dic2

两数之和
输入一个数字数组nums和一个目标target，若数组中存在两数x，y满足x+y==target，返回true，否则返回false

思路一：暴力求解，双重循环配对求和，时间复杂度O(N²)

思路二：将所有元素放入一个集合，先在外层循环每一个元素x，内层在Set里面查找target-x，找到了即返回对应下标

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> m;
        vector<int> res;
        for (int i = 0; i < nums.size(); ++i) {
            m[nums[i]] = i;
        }
        for (int i = 0; i < nums.size(); ++i) {
            int t = target - nums[i];
            if (m.count(t) && m[t] != i) {
                res.push_back(i);
                res.push_back(m[t]);
                break;
            }
        }
        return res;
    }
};

三数之和
顾名思义，若存在x+y+z==target，则返回true

思路一：三重循环，暴力求解。时间复杂度O(N³)

思路二：三重循环基础上改进，在前两重循环的基础上不再遍历z而是直接在Set里面查找target-(x+y)，时间复杂度O(N²·1)，空间复杂度O(N)（Set额外空间）

def threeSum(self, nums):
    if len(nums) < 3:
        return []
    nums.sort( )
    res = set( )
    for i, v in enumerate(nums[:-2]):
        if i >= 1 and V == nums[i-1]:
            continue
        d={}
        for X in nums [i+1:] :
            if x not in d:
                d[-v-x] = 1
            else:
                res.add((v, -v-x, x))
    return map(list,res)

思路三：循环+双指针法。先对数组排序，在一重循环遍历x的基础上，用一首一尾两个双指针两头逼近，查找y+z=target-x的情况。（升序排列情况下，若y+z < target-x，左指针右移，若y+z > target-x，则右指针左移，逆序排列反之）

def threeSum(self, nums):
    res =[]
    nums. sort()
    for i in xrange( len(nums)-2):
        if i > 0 and nums[i] == nums[i-1]:
            continue
        1, r = i+1, len(nums)-1
        while 1 < r:
            s = nums[i] + nums[U] + nums [r]
            if s<0: l+=1
            elif s>0:r-=1
            else:
                res . append( (nums[i], nums[U], nums[r]))
                while L < r and nums[l] == nums [l+1]:
                l+=1
                while L < r and nums[r] == nums [r-1]:
                    r -= 1
                l += 1; r -= 1
    return map(list,res)

四数之和

群体异位词给定一个字符串数组，找出数组中互为异位词的字符串并放到一个字数组中，最后返回所有异位词组合

思路一：使用set的方式存储异位词组，同一个key可有多个value。同时使用字符串内部排序的方式判断是否互为异位词。最后将set转化为array返回即可

var groupAnagrams = function(strs) {
    const map = new Map();
    for (let str of strs) {
        let array = Array.from(str);
        array.sort();
        let key = array.toString();
        let list = map.get(key) ? map.get(key) : new Array();
        list.push(str);
        map.set(key, list);
    }
    return Array.from(map.values());
};

技术

#算法 #学习进步

算法学习笔记第三讲

https://dockingyuan.top/2022/08/10/algorithm-3/

作者

Yuan Yuan

发布于

2022年8月10日

许可协议

算法学习笔记第四讲上一篇

算法学习笔记第二讲下一篇