算法学习笔记第二讲

复杂度分析与基本数据类型：数组/链表/堆栈/队列

算法复杂度

Big O Notation，也称“大O复杂度”，分为：

O(1): Constant Complexity: Constant 常数复杂度
O(log n): Logarithmic Complexity: 对数复杂度
O(n): Linear Complexity: 线性时间复杂度
O(n²): N square Complexity 平方
O(n³): N square Complexity 立方
O(2ⁿ): Exponential Growth 指数
O(n!): Factorial 阶乘

常见数据结构：

BigOCheatSheet复杂度：

根据主定理求解算法的复杂度：

Array

如下图所示，数组中所有元素在内存中连续存储：

查找根据下标直接取值，插入和删除需连续移动后续元素，复杂度：

Access: O(1)
Insert: 平均 O(n)
Delete: 平均 O(n)

LinkedList

插入操作（cur之后，新节点new）：

1
2
3

Node *new;
new->next=cur->next;
cur->next=new;

删除操作（pre之后的cur节点）：

1 2	`pre->next=pre->next->next; free(cur);`

复杂度：

prepend: O(1)
append: O(1)
lookup: O(n)
insert: O(1)
delete: O(1)

实战题目：

链表反转

思路：设定当前位置cur、前置指针pre，每次将cur的next指向pre，同时pre与cur后移

/**
 * Definition for singly-linked list.
    * struct ListNode {
    *     int val;
    *     ListNode *next;
    *     ListNode() : val(0), next(nullptr) {}
    *     ListNode(int x) : val(x), next(nullptr) {}
    *     ListNode(int x, ListNode *next) : val(x), next(next) {}
    * };
    */
   class Solution {
   public:
       ListNode* reverseList(ListNode* head) {
           ListNode* cur=head,*pre=NULL,*next=NULL;
           while(cur){
               next = cur->next;
               cur->next = pre;
               pre = cur;
               cur = next;
           }
           return pre;
       }
   };

做这道题时先看了Python的解法：

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution(object):
def reverseList(self, head):
    cur,pre=head,None
    while cur:
      cur.next,pre,cur = pre,cur,cur.next
    return pre

这里一行进行了多次变量赋值，如果拆开是不行的，cur.next需要先用一个temp指针记录下来

检测链表环

思路一：快慢指针，当链表中存在环，则一快一慢两指针必定会相遇

class Solution {
public:
bool hasCycle(ListNode *head) {
        if(!head || !head->next){
            return false;
        }
         ListNode *fast=head,*slow=head;
         while(slow && fast && fast->next){
             slow=slow->next;
             fast=fast->next->next;
             if(fast==slow){
                 return true;
             }
         }
         return false;
    }
};

思路二：集合判重。维护一个“经过集合”，每到一个节点，将节点加入集合。如果集合中已经存在该节点，则说明存在环。

var detectCycle = function(head) {
    let seen=new Set();
    while(head!=null){
        if(seen.has(head)){
            return true
        }
        seen.add(head);
        head=head.next;
    }
    return false;
};

两两交换链表中的节点

思路：备份链表头，设置元素对的前指针pre、中间指针cur和后指针next，每次分别修改pre指针指向next，next指向cur，cur指向原next的next，pre后移到cur（不会重复交换）

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* fakeHead = new ListNode(0);
        fakeHead->next = head;
        ListNode* pre = fakeHead;
        ListNode* cur=NULL ,*next=NULL;
        while (pre->next  && pre->next->next) {
            cur = pre->next;
            next = cur->next;
            pre->next = next;
            cur->next = next->next;
            next->next = cur;
            pre = cur;
        }
        return fakeHead->next;
    }
};

示意图：

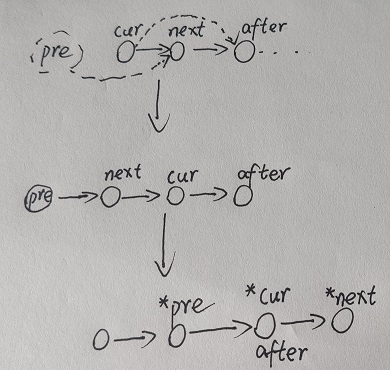
升级链表环，在检测链表环的基础上返回第一个进入环的节点。

思路：集合判重的方式

var detectCycle = function(head) {
    let seen=new Set();
    while(head!=null){
        if(seen.has(head)){
            return head
        }
        seen.add(head);
        head=head.next;
    }
    return null;
};

以k为组交换链表节点

思路：顾名思义，以k为组，反转子链，再把子链接起来

var reverseKGroup = function(head, k) {
    const hair = new ListNode(0);

    hair.next = head;
    fakehead=head
    let pre = hair;
    let len=0
    while(fakehead){
        fakehead=fakehead.next;
        len++;
    }

    while (head) {
        if(len<k) return hair.next // 查看剩余部分长度是否大于等于 k
        let tail = pre;
        for(let i=0;i<k;i++){//提取子串
            tail=tail.next
        }
   
        const nex = tail.next;
        [head, tail] = reverse(head, tail);
        // 反转子链接入主链
        pre.next = head;
        tail.next = nex;
        pre = tail;
        head = tail.next;
    
        len-=k
    }
    return hair.next;
};

const reverse=(head,tail)=>{
    let pre = tail.next;
    let p = head;
    while (pre !== tail) {
        const nex = p.next;
        p.next = pre;
        pre = p;
        p = nex;
    }
    return [tail, head];
}

Stack

First In First Out (FIFO)

实现方式：Array or Linked List

push与pop两种操作：

Queue

First In Last Out (FILO)
实现方式：Array or Linked List

元素进出示意图：

实战题目

用栈实现队列

思路：栈的特点是先入后出，队列的特点是先入先出，若要用栈实现队列则可用两个栈“联动”的方式实现。
- 维护一个input栈和一个output栈
- 新增元素的时候，直接压入input栈
- 弹出元素的时候，先看output是否为空，不为空直接弹栈，若为空则将input栈全部弹入output，再在output弹出

class MyQueue {
public:
    stack<int> input,output;
    int top;//临时全局变量栈顶元素
    MyQueue() {}
    
    void push(int x) {
        input.push(x);
    }
    
    int pop() {
        // 若output为空，则将input全部弹出并压入output中，然后output.pop()，后续push进入的还是要pop到output
        if (output.empty()) {
            while (!input.empty()) {
                top=input.top();
                output.push(top);
                input.pop();
            }
        }
        top=output.top();
        output.pop();
        return top;
    }
    
    int peek() {
        // 若output为空，则将input全部弹出并压入output中，然后output.peek()
        if (output.empty()) {
            while (!input.empty()) {
                top=input.top();
                output.push(top);
                input.pop();
            }
        }
        return output.top();
    }
    
    bool empty() {
        return output.empty() && input.empty();
    }
};

用队列实现栈
思路：

栈的特点是先入后出，队列是先入先出，若用队列实现栈，则需在元素入队后将元素逆置，让新元素维持在队列首，以前插入的在队列尾，这样出队的时候顺序就能反过来
可以用C++维护一个队列，新增元素入队时先入队，

c++版：

class MyStack {
public:
    queue<int> que;
    int len,front;//辅助全局变量len：队列长度,front：队首元素
    /** Initialize your data structure here. */
    MyStack() {}
    //压栈，需要根据栈长度，全部先弹出栈再压栈
    void push(int x) {
        len = que.size();
        que.push(x);
        for (int i = 0; i < len; i++) {
            que.push(que.front());
            que.pop();
        }
    }
    //通过front()获取元素，弹出直接pop即可
    int pop() {
        front = que.front();
        que.pop();
        return front;
    }
    //获取栈顶元素
    int top() {
        return que.front();
    }
    /** Returns whether the stack is empty. */
    bool empty() {
        return que.empty();
    }
};

JavaScript版：

var arr=[]
var MyStack = function() {
    arr=[]
};
MyStack.prototype.push = function(x) {
arr.push(x)
};
MyStack.prototype.pop = function() {
    if(arr.lenth>=1){
        return arr.pop()
    }
};
MyStack.prototype.top = function() {
    if(arr.length>=1){
        return arr[arr.length-1]
    }
};
MyStack.prototype.empty = function() {
    return arr.length==0
};

有效括号判断
左括号必须和右括号成对出现

思路一：

出现左括号，不能判别是否出现不匹配，只能先暂存处理；
出现右括号，则必须看左边括号是否相符，若相符则左边相邻括号，继续判断后续字符
使用栈，左括号压栈，右括号弹栈，到了字符串末尾判断栈是否为空

复杂度分析：弹栈/压栈操作的复杂度为O(1)，最坏情况每个字符串判断并操作一次，时间复杂度O(1)，空间复杂度O(n)

class Solution {
public:
    bool isValid(string s) {
        int len=s.length();
        if(len%2==1) return false;
        stack<char> closing;
        unordered_map<char, int> charmap = {//一个字符映射，目的是查找与右括号对应的字符
            {')','('},
            {']','['},
            {'}','{'}
            };
        for(int i=0;i<len;i++){
            if(s[i]=='('||s[i]=='{'||s[i]=='['){
                closing.push(s[i]);
            }
            else if(closing.empty() || charmap.find(s[i])->second!=(closing.top())){
                return false;
            }
            else{
                closing.pop();
            }
        }
        if(closing.empty()) return true;
        return false;
    }
};

这里一开始用的是map，后面改用unordered_map，前者是红黑树有序存放，后者基于哈希表无序排列，性能上更快。

思路二：

若括号能匹配，则字符串中必然有“()” “{}” “[]”等字符组合。
使用Java或JavaScript的replace函数，先将内层的、能直接匹配的括号对去掉
循环replace，将原来外围的括起来的括号对消去，当字符串长度不再变了停止循环，判断字符串是否为空

复杂度分析：最坏情况时间复杂度O(n²/2)，空间复杂度O(1)

class Solution {
    public boolean isValid(String s) {
        int len;
        do{
            len=s.length();
            if(len%2==1) return false;
            s=s.replace("()","").replace("{}","").replace("[]","");
        }while(len!=s.length());
        return (s.length()==0);
    }
}

技术

#算法 #学习进步

算法学习笔记第二讲

https://dockingyuan.top/2022/08/10/algorithm-2/

作者

Yuan Yuan

发布于

2022年8月10日

许可协议

算法学习笔记第三讲上一篇

算法学习笔记概述下一篇